堆:
1、概念
堆(二叉堆)可以视为一棵完全的二叉树,完全二叉树的一个“优秀”的性质是,除了最底层之外,每一层都是满的,这使得堆可以利用数组来表示(普通的一般的二叉树通常用链表作为基本容器表示),每一个结点对应数组中的一个元素。
如下图,是一个堆和数组的相互关系
堆和数组的相互关系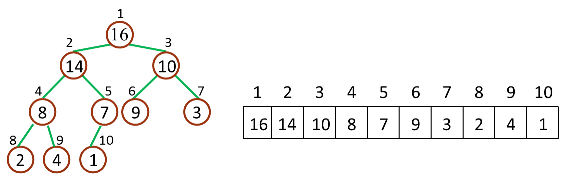
对于给定的某个结点的下标 i,可以很容易的计算出这个结点的父结点、孩子结点的下标:
Parent(i) = floor(i/2),i 的父节点下标
Left(i) = 2i,i 的左子节点下标
Right(i) = 2i + 1,i 的右子节点下标
需要注意的一个问题是:数组都是 Zero-Based,这就意味着我们的堆数据结构模型要发生改变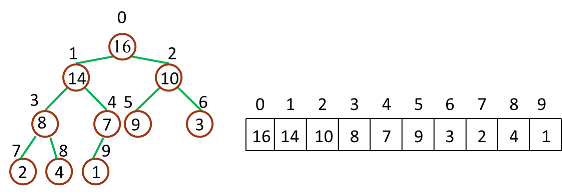
相应的,几个计算公式也要作出相应调整:
Parent(i) = floor((i-1)/2),i 的父节点下标
Left(i) = 2i + 1,i 的左子节点下标
Right(i) = 2(i + 1),i 的右子节点下标
2、堆的分类
二叉堆一般分为两种:最大堆和最小堆。
最大堆:
最大堆中的最大元素值出现在根结点(堆顶)
堆中每个父节点的元素值都大于等于其孩子结点(如果存在)最小堆:
最小堆中的最小元素值出现在根结点(堆顶)
堆中每个父节点的元素值都小于等于其孩子结点(如果存在)
3、堆的建立
堆的建立主要有两种方法,调整法和插入法;(1)调整法建大堆
将堆中所有数据重新排序,使其成为最大堆,其建堆的时间复杂度为O(n);
最大堆调整(MAX‐HEAPIFY)的作用是保持最大堆的性质,是创建最大堆的核心子程序,作用过程如图所示:
![MAX‐HEAPIFY-Procedure.png][4]
最大堆调整代码如下:
int a[10]={3,1,9,4,6,7,2,8,0,5};
void HeapAjust(int data[],int i,int length)
{
int nChild;
int nTemp;
for(nTemp=data[i];2*i+1<length;i=nChild)
{
nChild=2*i+1;
if(nChild<length-1&&data[nChild+1]>data[nChild])//比较哪个孩子比自己大,如果是右孩子的话,就要将 nChild++;
{
nChild++;
}
if(nTemp<data[nChild])//如果比自己的最大的孩子小,就交换
{
data[i]=data[nChild];
data[nChild]=nTemp;
}
else//如果比最大的孩子还大,就不交换
break;
}
}
堆建立代码如下:
for(int i=(10>>1)-1;i>=0;i--)
{
HeapAjust(data,i,length);//初始化一个堆
}
调整过程
i=4 3 1 9 4 6 7 2 8 0 5
i=3 3 1 9 8 6 7 2 4 0 5
i=2 3 1 9 8 6 7 2 4 0 5
i=1 3 8 9 4 6 7 2 1 0 5
i=0 9 8 7 4 6 3 2 1 0 5
需要注意的是,结点调整是从最后一个节点所在的父节点开始往上层调整;
(2)插入法建大堆
插入法建堆是将数组A中的元素逐个插入到数组B中建立一个堆。每插入一个关键字就与其父节点的关键字比较大小,如果 父节点的关键字较小则交换,然后依次自低地向上调整使之符合大(小)顶堆的特性,其建堆的时间复杂度为O(nlgn)。
插入法建堆与调整法建堆可能结果不一样。调整法建堆是自底向上依次调整,一棵子树中最大的节点值与根节点交换,最小的那个节点位置在本次调整中不作改变。而插入法建堆结果与插入的顺序和值大小有关。以大顶堆为例,在某棵已插入根节点的子树中,当插入左节点时,左节点与根节点交换,插入右节点时,右节点与根节点交换,那么这种情况下这颗子树三个节点的位置都发生改变了。而调整法建堆有一个节点位置不变,所以两种方法建堆结果可能不一样。
如输入为2、3、4,堆调整建堆为4、3、2,插入法建堆为4、2、3。
主要实现代码如下:
int a[10]={0};
int *size = 0;
void HeapAddajust(int*a , int*size , int val)
{
*size = *size+1;
int parent = *size/2;
int index = *size;
a[*size] = val;
while(a[index]<a[parent])
{
a[index] += a[parent];
a[parent] = a[index] - a[parent];
a[index] -= a[parent];
index = parent;
parent = index/2;
}
}
4、堆排序
堆排序是对已经组建的大堆或者小堆进行排序;
int a[10];//此处假设a已经是构建好的堆
int length = 10;
排序过程如下:
for(int j=length-1;j>0;--j)
{
int temp=a[j];
a[j]=a[0];
a[0]=temp;
HeapAjust(a,0,j);
}
说明:每次取最后一个节点与第一个节点进行交换,此时最后的一个节点为最大的节点了,之后从根节点对堆进行一次调整;一次循环结束后总节点数-1,继续交换和调整直到整个堆的节点都调整完即完成排序了。
